Esercizio applicando il 2° principio di Newton:

Calcolare di quanti metri si sposta un corpo di M = 500 kg tirato da una T = 5000N per un minuto lungo un piano orizzontale con coefficiente di attributo dinamico          μ= 0.2
Dati:
M = 500 kg     x = ?     ts = 1 mm (minuto)      μ= 0.2    T = 5000N     α = 45°   g = 9.80 m/s su s

1) Immagine illustrativa del problema:                                   2) Diagramma delle forze:      

    


3) 2° principio di Newton:                                                4) Scelgo il sistema di riferimento:

                                                                                
         










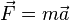
5) Coordinate dei vettori: Fn = (0;Fn)   Fa = (Fa;0)   P = (0;-M x g)   T = (Tcos45°;Tsen 45°)

6) Eq. di Newton lungo l'asse z: 
Fn + 0 - Mg + Tsen45° = M x a2
a2 = 0
Fn = Mg - Tsen45° = 500 x 9.80 - 5000 x 0.707 = 4900 - 3535 = 1365N                          

7) Eq. di Newton lungo l'asse x:                            
0 - Fa + 0 + Tcos45° = Max
Max = Tcos45° - Fa = Tcos45° - μFn = 5000 x 0.707 - 0.2 x 1365 = 3535 - 273 = 3262N
ax = 3262/500 = 6.524 m/s su s  

8) Moto uniformemente accelerato:
S= So + Vo t + 1/2at^2, lungo asse x:
x = 0 + 0 +1/2axt^2       x=1/2axt^2
Δx = 1/2 x 6.524 x 60^2 = 11743m