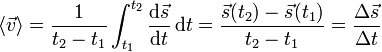Tutta fisica...

mercoledì 1 giugno 2011

Statica

La statica studia l’equilibrio dei corpi. Un corpo è in equilibrio se è fermo e persevera nel suo stato di quiete al trascorrere del tempo. Un modello è la semplificazione di una situazione reale, utile per concentrare lo studio su alcuni aspetti di un fenomeno, ignorandone altri. Il punto materiale è il modello di un corpo reale, ed è un punto in cui si immagina concentrata tutta la materia presente nel corpo. Esso è utile quando il corpo reale si può considerare di dimensioni trascurabili rispetto al contesto in cui si trova, e tutte le forze possono essere considerate applicate nello stesso punto. Il punto materiale non ha dimensioni, e può solo effettuare moti traslatori; inoltre ha una massa e quindi una forza peso. Il vincolo è un impedimento che limita parzialmente o totalmente il moto di un corpo; la reazione vincolare è la forza che il vincolo esercita su tale corpo, ed è una forza di tipo elastico e di natura elettromagnetica. La condizione di equilibrio di un punto materiale ( detta anche I equazione cardinale della statica) è la seguente: un punto materiale è in equilibrio se è nulla la somma vettoriale di tutte le forze applicate ad esso, comprese le reazioni vincolari.

Se sul punto materiale agisce una sola forza non può essere in equilibrio: l’effetto della forza è il pavimento del punto.

Se invece vi sono applicate due forze il punto è in equilibrio, allora le due forze sono uguali e opposte.

In genere, punto è in equilibrio quando la risultante di tutte le forze applicate è nulla.

forza risultante su una pallina: a 0

F risultante sulla pallina = 0

2 forze: gravità e vincolare. Il tavolo applica questa forza opposta a quella di gravità.

Un corpo è in equilibrio quando la F gravità – F vincolare = 0; la forza risultante è uguale a 0.

La forza equilibrante

Quando un punto materiale non è in equilibrio, per equilibrarlo basta applicare una forza uguale e opposta alla risultante delle forze applicate. Viene chiamata forza equilibrante

Punto materiale vincolato.

Piano inclinato.

Forza di gravità spezzata in 2 forze: una perpendicolare e una parallela.

Una la tiene incollata al piano e l’altra la fa cadere.

Per farla fermare devo applicare una forza opposta a quella parallela.

Il punto su un piano inclinato non è in equilibrio anche se è vincolato a stare sul piano.. infatti l’azione forza peso si esercita in due modi: tiene premuto il punto contro il piano e contemporaneamente lo spinge lungo il piano.

L’unica forza che fa muovere il punto è la componente parallela. In generale per tenere in equilibrio un punto su un piano inclinato basta equilibrare la componente parallela del peso con una forza uguale e opposta.

Fe = -P11

L’attrito dinamico

Una biglia che ruota in un pavimento dopo un po’ si ferma.

In ogni caso la velocità diminuisce progressivamente perché le piastrelle del pavimento interagiscono con il corpo, dando luogo a una forza di contatto. Si chiama forza di attrito dinamico.

Nella realtà una superficie completamente liscia non si può avere; presenta sempre delle asperità: atrito tra superficie pallina e pavimento: forza di atrito.

Tra pallina e pavimento: atrito dinamico.

Quando due corpi si muovono mantenendosi a contatto l’uno con l’altro, su di ciascuno di essi si esercita una forza di atrito che ostacola il pavimento relativo.

È utile ad. Esempio quando bisogna frenare in auto o in bicicletta. Ma dannoso nei motori perché produce l’usura delle parti meccaniche.

Il corpo rigido di un oggetto ideale che mantiene la stessa forma e le stesse dimensioni qualunque sia la sollecitazione cui lo sottopone. Il corpo rigido può essere pensato come scomponibile in un grande numero di punti materiali, ed i movimenti di cui esso è capace possono a loro volta essere interpretati come moti d’insieme dei punti materiali che lo costituiscono. Studieremo il moto di traslazione ed il moto di rotazione di un
corpo rigido e la loro composizione, tralasciando l’analisi di movimenti più complessi come quello di imperniamento. Si dice che un corpo rigido compie un moto di traslazione se tutti i suoi punti si muovono con lo stesso vettore velocità. Si dice che un corpo rigido compie un moto di rotazione se tutti i suoi punti descrivono delle circonferenze con centro sulla retta, che è detta asse di rotazione. E’ importante sottolineare che un moto di traslazione non implica necessariamente che i punti materiali che compongono il corpo rigido si muovano su delle traiettorie rettilinee: essi potranno compiere anche dei tratti curvi, od al limite delle circonferenze. L’importante è che non siano concentriche. Lo spostamento di un corpo rigido può sempre essere scomposto applicando a tutto il corpo dapprima la traslazione subita da un qualunque suo punto e successivamente una rotazione attorno ad un asse passante per tale punto.

domenica 8 maggio 2011

Esercizio applicando il 2° principio di Newton:

Calcolare di quanti metri si sposta un corpo di M = 500 kg tirato da una T = 5000N per un minuto lungo un piano orizzontale con coefficiente di attributo dinamico μ= 0.2
Dati:
M = 500 kg x = ? ts = 1 mm (minuto) μ= 0.2 T = 5000N α = 45° g = 9.80 m/s su s

1) Immagine illustrativa del problema: 2) Diagramma delle forze:

3) 2° principio di Newton: 4) Scelgo il sistema di riferimento:

$\vec{F} = m \vec{a}$

5) Coordinate dei vettori: Fn = (0;Fn) Fa = (Fa;0) P = (0;-M x g) T = (Tcos45°;Tsen 45°)

6) Eq. di Newton lungo l'asse z:
Fn + 0 - Mg + Tsen45° = M x a2
a2 = 0
Fn = Mg - Tsen45° = 500 x 9.80 - 5000 x 0.707 = 4900 - 3535 = 1365N

7) Eq. di Newton lungo l'asse x:
0 - Fa + 0 + Tcos45° = Max
Max = Tcos45° - Fa = Tcos45° - μFn = 5000 x 0.707 - 0.2 x 1365 = 3535 - 273 = 3262N
ax = 3262/500 = 6.524 m/s su s

8) Moto uniformemente accelerato:
S= So + Vo t + 1/2at^2, lungo asse x:
x = 0 + 0 +1/2axt^2 x=1/2axt^2
Δx = 1/2 x 6.524 x 60^2 = 11743m

giovedì 5 maggio 2011

Dinamica:

Fino a circa 400 anni fa, lo studio del moto era impostato su criteri spesso più filosofici che scientifici. Ad esempio, nella concezione aristotelica, la caduta verso il suolo di una palla di cannone era interpretabile come la manifestazione, o la conseguenza, di una tensione del corpo verso la sua posizione naturale; agli oggetti celesti, il Sole, la Luna e le stelle, si attribuiva un moto circolare intorno alla Terra, perché ritenuto il moto perfetto.

Al fisico e astronomo Galileo Galilei si deve il merito di aver cominciato ad analizzare il moto dei corpi con criteri scientifici, in termini di spostamenti compiuti a partire da una data posizione iniziale, in un determinato intervallo di tempo. Egli mostrò che la velocità di un corpo in caduta libera aumenta a un ritmo costante nel corso della caduta e che questo ritmo, se si trascurano gli effetti dell'attrito, è uguale per tutti i corpi.
Il matematico e fisico inglese Isaac Newton definì rigorosamente i concetti di forza, massa e accelerazione ed enunciò il principio, noto oggi come seconda legge della dinamica, che descrive la relazione esistente tra queste grandezze. Le leggi di Newton sono tuttora valide per la descrizione dei fenomeni ordinari; sono invece inappropriate a descrivere il moto dei corpi dotati di velocità prossime a quella della luce, per i quali fu concepita la teoria della relatività di Albert Einstein, e il comportamento delle particelle atomiche e subatomiche, che sono invece oggetto di studio della teoria quantistica.

I principi della dinamica:

La prima legge di Newton
La prima legge del moto, nota anche come primo principio della dinamica, afferma che in assenza di forze agenti, un corpo conserva il proprio stato di quiete (resterà immobile) o di moto rettilineo uniforme (continuerà a viaggiare in linea retta mantenendo sempre la stessa velocità).La prima legge di Newton è detta anche principio d'inerzia.

La seconda legge di Newton
La seconda legge del moto stabilisce che una forza applicata a un corpo (indeformabile) gli imprime una accelerazione a essa proporzionale, e può essere espressa dalla relazione

F = ma
La costante di proporzionalità è la massa inerziale del corpo.
La terza legge di Newton
La terza legge del moto afferma che quando un corpo esercita una forza su un altro corpo, quest'ultimo reagisce esercitando sul primo una forza uguale e contraria.
La terza legge di Newton è detta anche principio di azione-reazione.

sabato 30 aprile 2011

Moto di un proietile

Siamo ora in grado di studiare un classico esempio di cinematica: il moto del proiettile. Il problema e' quello di lanciare un corpo sulla superficie della Terra, con una velocita' iniziale ${\bf v_0}$ e determinare il tipo di moto che ne consegue. Notiamo che il simbolo delle velocita' e' scritto in grassetto, quindi e' un vettore. Questo vuol dire che la direzione di lancio formera' un certo angolo con la linea orizzontale della Terra. Scegliamo ora un sistema di riferimento in cui l'asse x sia orientato lungo la superficie della Terra mentre l'asse z sia perpendicolare ad esso e rivolto verso l'alto come mostrato in figura 1.14.2. Supponiamo anche, per semplicita', di lanciare il corpo dall'origine del sistema di riferimento.

**Figura 1.14.2:** *La velocita' iniziale del moto del proiettile.*
$\begin{figure}\par \vspace{-2cm} \par \begin{center} \par \epsfig{file=fig_pro.e... ...ght=12cm,width=12cm} \par \vspace{-1cm} \par\par \end{center}\par \end{figure}$

Come si risolve questo tipo di problemi in cui il moto non si svolge piu' su una retta? Il metodo e' molto semplice: proiettare il moto lungo i due assi e studiarli indipendentemente l'uno dall'altro. Se proiettiamo il vettore velocita' lungo i due assi otterremo:

$\begin{displaymath}V_{0x} = V_0 cos \alpha \qquad (1)\end{displaymath}$

$\begin{displaymath}V_{0z} = V_0 sin \alpha \qquad (2)\end{displaymath}$

Quindi dobbiamo immaginare che e' come lanciare due corpi, uno lungo l'asse x, con una velocita' iniziale $V_{0x}$ e l'altro lungo l'asse z con velocita' iniziale $V_{0z}$ . Che tipo di moto seguiranno questi corpi? Abbiamo osservato nel capitolo 13 che tutti i corpi lanciati verso l'alto sono sottoposti ad una accelerazione di gravita' rivolta verso il basso. Il moto lungo la verticale sara' quindi un moto uniformemente accelerato. Quindi le equazioni che descrivono il moto lungo z saranno:

$\begin{displaymath}V_z = V_{0z} - g t\end{displaymath}$

$\begin{displaymath}z = V_{0z} t - g \frac{t^2}{2} \qquad (3)\end{displaymath}$

Lungo l'asse x invece non vi e' alcuna accelerazione, poiche' l'accelerazione di gravita' e' perpendicolare alla superficie della Terra. Accelerazione nulla vuol dire velocita' costante per cui il moto lungo l'asse x sara' un moto rettilineo uniforme. Le equazioni che descrivono questo moto lungo l'asse x sono quindi:

$\begin{displaymath}Vx = V_{0x}\end{displaymath}$

$\begin{displaymath}x = V_{0x} t \qquad (4)\end{displaymath}$

Possiamo ora collegare questo insieme di equazioni per calcolare la traiettoria del corpo. Una traiettoria e' l'insieme dei punti occupati dal corpo nel suo moto. Per ottenerla eliminiamo il tempo dalle precedenti equazioni. Dalla (4) otteniamo:

$\begin{displaymath}t = \frac{x}{V_{0x}}\end{displaymath}$

e, sostituendo nella (3):

$\begin{displaymath}z = V_{0z}\frac{x}{V_{0x}} - \frac{g}{2}(\frac{x}{V_{0x}})^2\end{displaymath}$

che si puo' anche scrivere:

$\begin{displaymath}z = \frac{V_{0z}}{V_{0x}} x - \frac{g}{2 V_{0x}^2} x^2 \qquad(5)\end{displaymath}$

che e' l'equazione di una parabola del tipo:

. Quindi, la traiettoria descritta dal corpo e' una parabola.
Utilizzando ora le equazioni (1,2) possiamo anche scrivere la (5) come:

$\begin{displaymath}z = tg \alpha x - \frac {g}{2 V_0^2 cos^2 \alpha} x^2 \qquad (6)\end{displaymath}$

dove compaiono esplicitamente la velocita' iniziale e l'angolo formato dalla velocita' iniziale con l'asse x.

Fig. 2.14.2 Il moto del proiettile. I cursori velocita' e angolo permettono di modificare i parametri di lancio del proiettile. Il cursore "vettori" evidenzia le componenti della velocita' del proiettile.

mostra una simulazione del moto del proiettile. L'angolo di lancio e la velocita' iniziale possono essere modificati mediante i due cursori. Il pulsante ``Velocita''' mostra il vettore velocita' insieme alle sue componenti lungo gli assi. Notiamo che la velocita' verticale cambia costantemente come accade nel moto uniformemente accelerato, mentre la velocita' orizzontale rimane costante.

Le equazioni (5) o (6) possono essere utilizzate per calcolare la gittata, ovvero la distanza fra il punto di lancio e il punto di caduta. Il punto di caduta e' semplicemente il punto in cui z = 0. Imponendo questa condizione nella (5) otteniamo:

$\begin{displaymath}0 = \frac{V_{0z}}{V_{0x}} x - \frac{g}{2 V_{0x}^2} x^2\end{displaymath}$

oppure, mettendo in evidenza x:

$\begin{displaymath}0 = x(\frac{V_{0z}}{V_{0x}} - \frac{g}{2 V_{0x}^2} x)\end{displaymath}$

Questa espressione diventa nulla quando x=0 (questa condizione non ci serve, e' solo il punto di partenza) oppure quando il termine nelle parentesi diventa nullo, ovvero:

$\begin{displaymath}\frac{V_{0z}}{V_{0x}} = \frac{g}{2 V_{0x}^2} x\end{displaymath}$

Semplificando:

$\begin{displaymath}V_{0z} = \frac{g}{2 V_{0x}} x\end{displaymath}$

e da questa possiamo ottenere l'espressione della nuova intersezione della parabola con l'asse x che chiameremo gittata:

$\begin{displaymath}x_g = \frac{2 V_{0z}V_{0x}}{g} \qquad (7)\end{displaymath}$

Tenendo presenti le (1):

$\begin{displaymath}x_g = \frac{2 V_0^2 sin \alpha cos \alpha}{g}\end{displaymath}$

e che $sin 2 \alpha = 2 sin \alpha cos \alpha$ otteniamo l'espressione finale della gittata:

$\begin{displaymath}x_g = \frac{V_0^2 sin 2 \alpha}{g} \qquad(8)\end{displaymath}$

Questa equazione si puo' utilizzare per calcolare, dato un certo valore della velocita' iniziale

, per quale angolo di tiro un corpo raggiunge la distanza massima. Nella (8), basta calcolare il valore massimo di $sin 2 \alpha$ che e' 1. Il seno di un angolo e' 1 a

, quindi deve essere $2 \alpha = 90^0$ ovvero:

$\begin{displaymath}\alpha = 45^0\end{displaymath}$

Possiamo ora calcolare il tempo di volo, ovvero il tempo impiegato dal proiettile a percorrere interamente la sua traiettoria. Un metodo semplice per ottenerlo e' quello di osservare la proiezione del moto lungo l'asse x, che si svolge con moto uniforme. In un tempo di volo $\tau$ la proiezione del corpo sull'asse delle ascisse percorrera' una distanza pari alla gittata con una velocita' $V_{0x}$ , quindi:

$\begin{displaymath}V_{0x} = \frac{x_g}{\tau}\end{displaymath}$

dalla quale si ottiene, tenendo presente la (7):

$\begin{displaymath}\tau = \frac{x_g}{ V_{0x}} = \frac{2 V_{0z}}{g}\end{displaymath}$

domenica 27 febbraio 2011

Accelerazione

L'accelerazione e la variazione della velocità del moto. Si tratta di una grandezza vettoriale, dotata non solo di un valore scalare ma anche di direzione.

L'accelerazione può essere causata non solo dalla variazione della velocità, ma anche da un cambiamento della direzione lungo la quale si svolge il moto. In questo caso si parla di accelerazione centrifuga.

Moto uniformamente accelerato:

Nel moto uniformemente accelerato la velocità varia in modo regolare con il passare del tempo.La velocità in un determinato istante di tempo è proporzionale al tempo trascorso:

v=at

L'accelerazione è costante.

La relazione tra lo spazio percorso e il tempo, cioè la legge oraria è:

s=(1/2)at²

Se rappresentiamo in un grafico la legge oraria, otteniamo una parabola. Il fatto che la curva diventi sempre più ripida rispecchia il continuo

della velocità.

Il moto circolare uniforme:

Il moto circolare uniforme è un moto a velocità scalare costante lungo una circonferenza.
Anche se la velocità ha un valore scalare costante, in realtà essa cambia di direzione lungo la traiettoria. Esiste allora una accelerazione, dovuta ad un cambiamento della direzione del moto che si chiama accelerazione centrifuga, diretta verso l'esterno. L'accelererazione centripeta è uguale come valore ma diretta verso l'interno.

Quando in automobile percorriamo una curva sentiamo l'effetto della forza centrifuga, e la forza centripeta, uguale e contraria, è quella che ci tiene legati alla strada e ci consenete percorrere la curva.

venerdì 4 febbraio 2011

Velocità

Si usa il termine velocità per descrivere in moto, ma, parlando, si considera la velocità una grandezza scalare: il rapporto tra la distanza percorsa e il tempo impiegato. In Fisica, invece, la velocità è una grandezza vettoriale che considera la distanza, tempo e direzione. La formula della velocità è $\displaystyle\blue{v}=\frac{{S}}{{t}}$ dove s si misura in metri e t si misura in secondi, l'unità di misura della velocità è m/s. esistono però anche delle formule inverse $\displaystyle\blue{t}=\frac{{S}}{{v}}$ e $\displaystyle\blue{S}={v}\cdot{t}$ .

Se un'auto viaggia a velocità scalare costante in linea retta, ha una velocità vettoriale costante. Se viaggia su una strada tortuosa, la velocità scalare può essere costante, ma la velocità vettoriale varia a ogni cambiamento di direzione.

la velocità si divide in:

velocità media: rapporto tra lo spostamento e la durata dell'intervallo di tempo impiegato a percorrerlo:

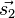$\vec {v} = \frac {\vec {s_2}-\vec {s_1}}{t_2-t_1} = \frac {\Delta \vec {s}}{\Delta t}$

dove $\Delta\vec {s}=\vec {s_2}-\vec{s_1}$ è lo spostamento, $\vec {s_2}$ e $\vec {s_1}$ sono i vettori posizione e

Δ t = t 2 - t 1

è l'intervallo di tempo impiegato ad effettuare lo spostamento;

velocità istantanea: limite della velocità media per intervalli di tempo molto brevi ovvero derivata della posizione rispetto al tempo:

$\vec {v} = \lim_{t\to t_0}\frac {\vec {s}(t)-\vec {s}(t_0)}{t-t_0}=\frac {\operatorname {d}\vec {s}}{\operatorname {d} t}$ .

La velocità media è proprio la media della velocità istantanea in uno tempo finito

Δ t = t 2 - t 1

$\langle \vec v \rangle=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}\frac{\mathrm{d}\vec s}{\mathrm{d}t}\,\mathrm{d}t = \frac{\vec s(t_2)-\vec s(t_1)}{t_2-t_1}=\frac{\Delta\vec s}{\Delta t}$

La velocità scalare media è una grandezza scalare ed è definita come lo spazio totale percorso diviso il tempo impiegato:

$\langle v_s \rangle = \frac{\Delta s}{\Delta t}$

Si noti come questa definizione sia molto diversa dalla velocità vettoriale media, per esempio nel moto circolare, cioè il moto che avviene lungo una circonferenza, dopo un periodo T, cioè dopo aver fatto un giro, la velocità vettoriale è nulla, perché il punto di arrivo e quello di partenza coincidono ( $\Delta\vec s=0$ ), mentre la velocità scalare media è uguale a $\frac{2\pi R}{T}$ con R il raggio della circonferenza.

Moto rettilineo uniforme:

Un automobile che si muove a velocità costante senza mai cambiare direzione si muove di moto rettilineo uniforme.
Lo spazio S percorso dall'automobile è allora proporzionale al tempo impiegato per percorrerlo:

S = VT

e la costante di proporzionalità è la velocità Vdell'automobile.
La relazione tra spazio e tempo nel moto di un oggetto si chiama legge oraria.

Nel grafico possiamo osservare che se la velocità aumenta, aumenta la pendenza della retta.